Luciano Demasi is the author of the book “Introduction to Unsteady Aerodynamics and Dynamic Aeroelasticity” (Springer, 2024, DOI 10.1007/978-3-031-50054-1,
https://link.springer.com/book/10.1007/978-3-031-50054-1).

Luciano Demasi has written a comprehensive and insightful book on aeroelasticity as practiced today. The careful and deep attention to the fundamentals and a unique and valuable discussion of the implementation of Doublet Lattice aerodynamics are special features of the book. The author also ranges over a number of additional topics including current and promising aircraft and wing concepts that bring new challenges to the aeroelastician.
The student new to the topic as well as the experienced practitioner will find much to ponder and benefit from a careful reading of this text.
— Prof. Earl Dowell, Duke University
This book represents a comprehensive treatment of unsteady aerodynamics and dynamic aeroelasticity, covering the fundamentals of unsteady aerodynamics and dynamic aeroelasticity in 831 pages, 39 chapters and 18 appendices. It explains the fundamentals of the doublet lattice method and its applications, introduction to nonlinear aeroelasticity, including the effects of control surface free play giving rise to limit cycle oscillations. It further discusses techniques for mapping the structural vibration mode shapes from a finite element mesh to the corresponding aerodynamic mesh, and methods of determining the flutter point. Each chapter includes a list of competency questions which makes it very useful for teaching the subject. In short, it is an excellent textbook for teaching the subject of aeroelasticity, and a very useful reference for practicing aerospace engineers.
— Prof. Gautam SenGupta, University of Washington, Bothell, WA, and Boeing Technical Fellow (Retired)
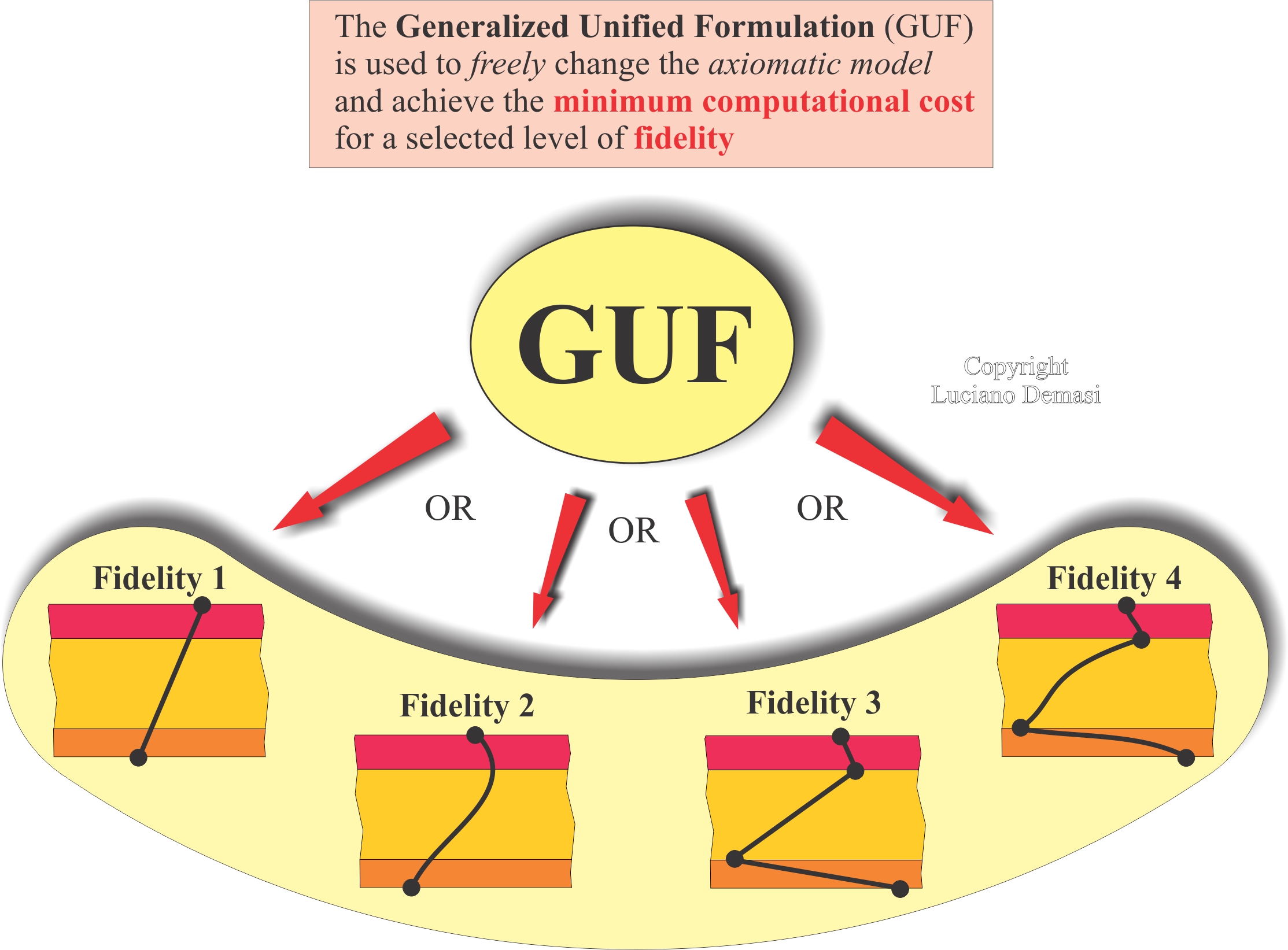
Fundamental Modeling of Structures
Dr. Demasi introduced the Generalized Unified Formulation (GUF) theory-invariant computational architecture for the analysis of multilayered structures and assessed numerical performance and problems of mixed formulation (Reissner’s Mixed Variational Theorem). For this research he received a “best paper of the year” award (Composite Structures Journal, 2010), and a series of five papers was published at once without requests for changes. This work was highly praised by the journal reviewers as shown below:
“A major and timely treatise on composite plate theories which will be widely welcomed by the composites community. An easy to understand comparison of composite plate analytical methodologies which succinctly explains the subtleties in more complex problems”.
“An exceptional contribution to knowledge in laminated plate theory which deserves a wide audience.
The most outstanding contribution to composite structures this reviewer has had the pleasure of assessing for some time”.
“May I add that I greatly enjoyed reading your papers and am sure that they will be widely appreciated. They break new ground in being the first series of five papers since the Journal began 25 years ago. Also although occasionally papers are accepted for publication without changes being required, this is unusual. It is very unusual for a series of two papers to be accepted in this way, which makes a series of five “exponentially unlikely!”
Selected Publications
Mechanics of Advanced Materials and Structures, Vol. 17, 20-39, 2010, DOI: 10.1080/15376490802665684
Composite Structures, Vol. 84, 256-270, 2008, DOI: 10.1016/j.compstruct.2007.08.004
- L. Demasi, “Invariant Finite Element Model for Composite Structures: the Generalized Unified Formulation”, AIAA Journal, Vol. 48, No. 8, 2010, DOI: 10.2514/1.45416
- Demasi, “∞6mixed plate theories based on the Generalized Unified Formulation. Part I: Governing Equations”, Composite Structures, Vol. 87, 1-11, 2009,
DOI: 10.1016/j.compstruct.2008.07.013
- Demasi, “∞6mixed plate theories based on the Generalized Unified Formulation. Part II: Layerwise theories”, Composite Structures, Vol. 87, 12-22, 2009,
DOI: 10.1016/j.compstruct.2008.07.012
- Demasi, “∞6mixed plate theories based on the Generalized Unified Formulation. Part III: Advanced Mixed High Order Shear Deformation Theories”, Composite Structures, Vol. 87, 83-194, 2009, DOI: 10.1016/j.comstruct.2008.07.01
- Demasi, “∞6mixed plate theories based on the Generalized Unified Formulation. Part IV: Zig-Zag Theories”, Composite Structures, Vol. 87, 195-205, 2009,
DOI: 10.1016/j.compstruct.2008.07.010
Composite Structures, Vol. 88, 1-16, 2009, DOI: 10.106/j.compstruct.2008.07.009
- Demasi, “2D, Quasi 3D and 3D Exact Solutions for Bending of Thick and Thin Sandwich Plates”, Journal of Sandwich Structures & Materials, Vol.10, No. 4, 271-310,
DOI: 10.1177/1099636208089311, 2008
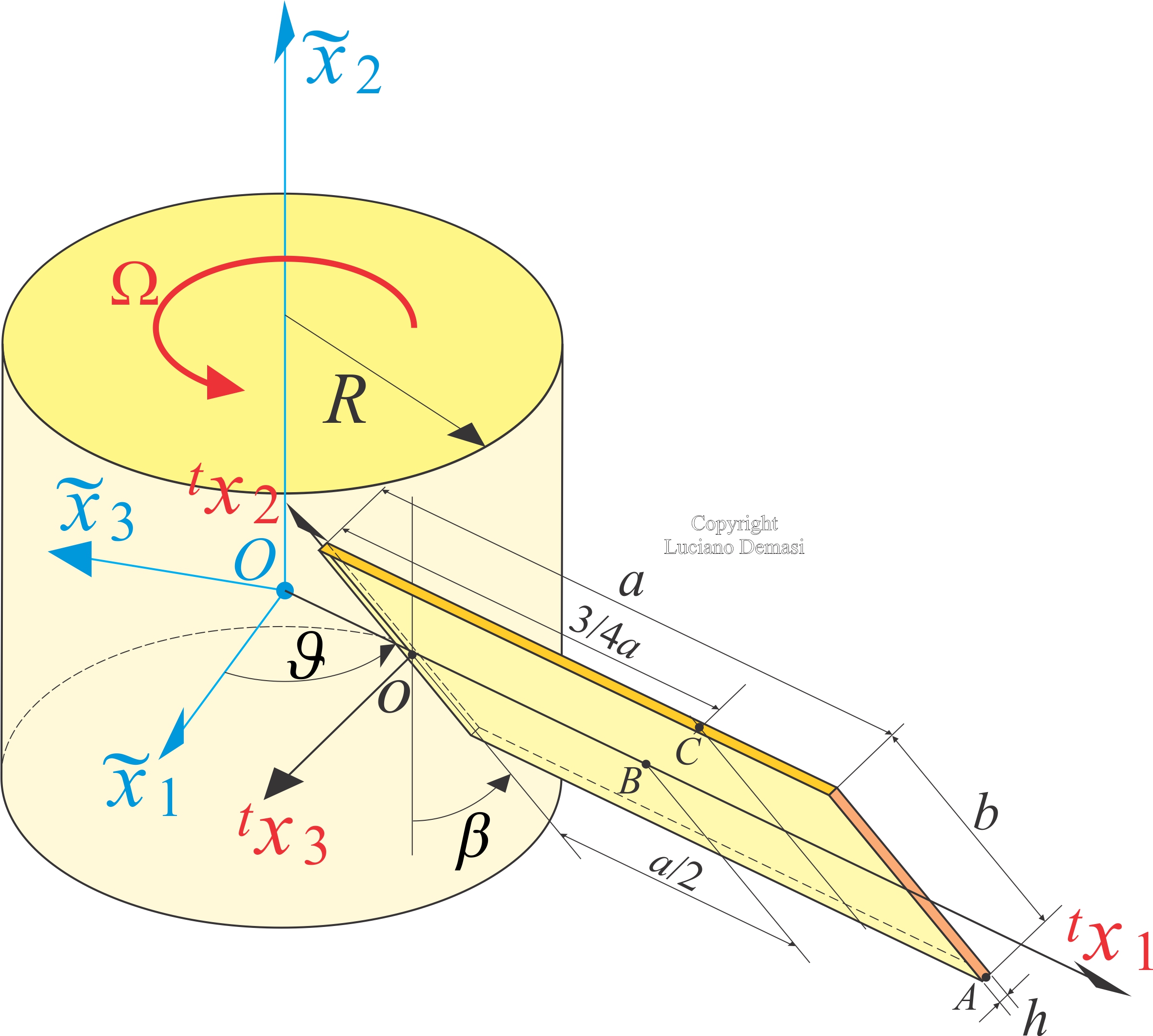
Large Displacement Analysis of Composite Structures and Variable Angle Tows
Murakami’s Zig-Zag Function in conjunction of Green-Lagrange Strain– and Second-Piola Kirchhoff Stress-tensors and Generalized Unified Formulation were introduced to present Zig-Zag theories for composite structures. Special stress recovery procedure for an accurate determination of the transverse stresses was also presented.
Large displacement modal and transient analysis of rotating plates was also performed with the use of Murakami’s Zig-Zag model.
Selected Publications
- Santarpia, C. Testa, L. Demasi, L. Greco, G. Bernardini, “A Hierarchical Generalized Formulation for the Large-Displacement Dynamic analysis of Rotating Plates”, Computational Mechanics, 2021, issue 6, DOI: 10.1007/s00466-021-02070-w
- Santarpia, L. Demasi, “Large Displacement Models for Composites Based on Murakami’s Zig-Zag function, Green-Lagrange Strain Tensor, and Generalized Unified Formulation”, Thin-Walled Structures, 2020, Vol. 150
- Demasi, G. Biagini, F. Vannucci, E. Santarpia, R. Cavallaro, “Equivalent Single Layer, Zig-Zag and Layerwise Theories for Variable Angle Tow Composite Based on the Generalized Unified Formulation”, Composite Structures, Vol. 177, pp. 54-79, 2017, DOI: 10.1016/j.compstruct.2017.06.033
- Demasi, Y. Ashenafi, R. Cavallaro, E. Santarpia “Generalized Unified Formulation Shell Element for Variable-Stiffness Composite Laminates and Aeroelastic Applications”, Composite Structures, Vol. 131, pp. 501-515, 2015, DOI: 10.1016/j.compstruct.2015.05.022
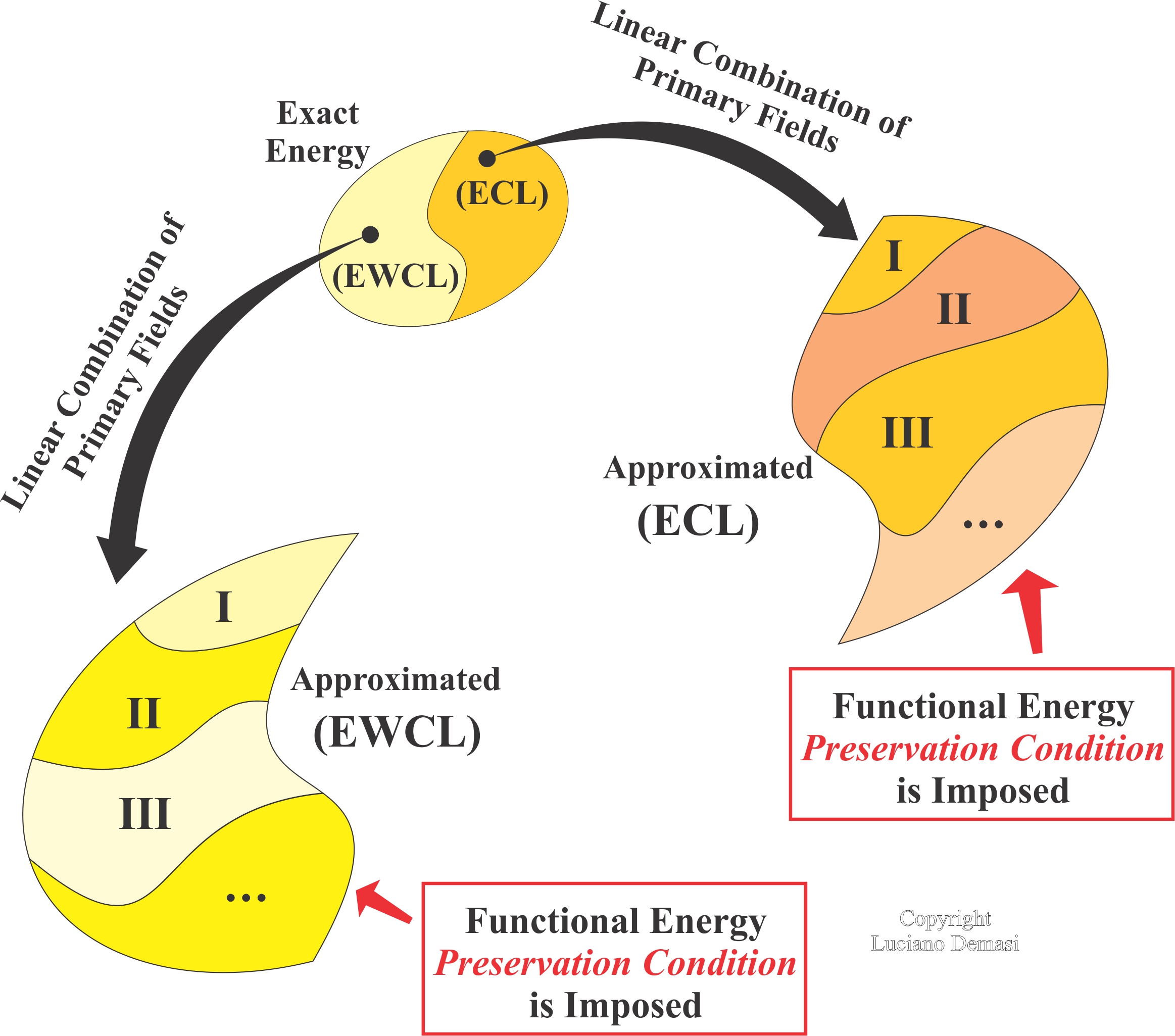
Partitioned Parametrized Variational Procedure for the Generation of Theorems of Structural Analysis
Structural field modeling of displacements, stresses, and strains is linked with the generation of functionals. Dr. Demasi introduced the Partitioned Parametrized Variational Procedure (PPVP). In-plane stresses and strains are mathematically treated differently than the transverse counterparts. This allows the generation of all the classical variational theorems of elasticity (Principle of Virtual Displacements and Complementary Energy, Hellinger-Reissner Principle, Reissner’s Mixed Variational Theorem, and the Veubeke-Hu-Washizu theorem) and an infinite number of new variational theorems that can be used for the solutions of various structural problems and multifield analyses.
Selected Publications
- Demasi “Properties and Layerwise Moideling of the Harlequin Variational Theorem for Composite Structures”, Mechanics of Advanced Materials and Structures, 1-30,
https://doi.org/10.1080/15376494.2023.2260554, 2023
- Demasi “Partitioned Parametrized Variational Procedure for the Generation of Theorems of Structural Analysis”, Mechanics of Advanced Materials and Structures, 1-20,
https://doi.org/10.1080/15376494.2022.2044098, 2022
Physical Understanding of Nonlinear Dynamic Aeroelastic Response of Joined Wings
Dr. Demasi and co-authors worked on the field of nonlinear aeroelasticity of Joined Wings for 2 decades and received for one of his papers the Collier Research HyperSizer American Institute of Aeronautics and Astronautics Structures best paper award.
The scientific contributions in that area can be summarized as follows:
- Introduced the concept of “snap divergence” to explain the static aeroelastic stability properties of Joined Wings and showed how to interpret experimental work available in the literature.
- Showed the relevant effect of the “aeroelastic tailoring” by changing the instability mechanism (buckling and post-buckling responses).
- Demonstrated that the geometric nonlinearities must be included in Joined Wings even for “apparently small” deformation in order to correctly predict the response.
- Showed the highly complex phenomena that may take place for a given freestream velocity when Joined Wings are considered: unstable branches, stable branches, Hopf’s bifurcation, Limit Cycle Oscillation, Flip bifurcation, Bi-cyclic orbit etc.
- Demonstrated with an energy interpretation, that the freeplay can even disrupt the energy injection into the structure by the flow and, thus, the flutter instability may be postponed.
- Interpreted when “body freedom flutter” and “cantilever flutter” occur in realistic Joined Wing configuration.
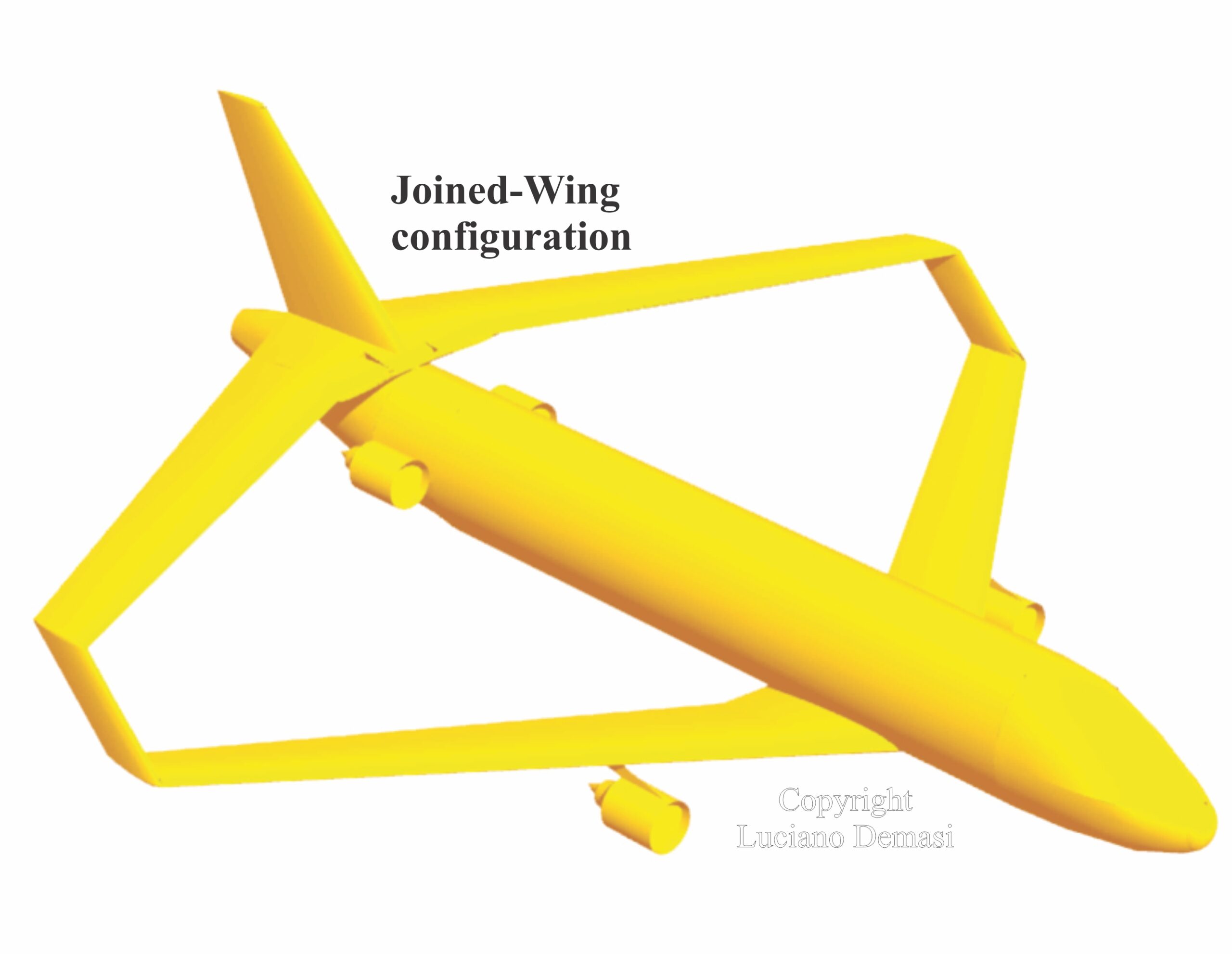
Selected Publications
- Cavallaro, L. Demasi “Challenges, Ideas, and Innovations of Joined-Wing Configurations: A Concept from the Past, an Opportunity for the Future”, Progress in Aerospace Sciences, Vol. 87, pp. 1-93, 2016, DOI: 10.1016/j.paerosci.2016.07.002
- Cavallaro, R. Bombardieri, L. Demasi, A. Iannelli “PrandtlPlane Joined Wing: Body Freedom Flutter, Limit Cycle Oscillation and Freeplay Studies”, Journal of Fluids and Structures, Vol. 59, No. 11, pp. 57-84, 2015, DOI: 10.1016/j.jfluidstructs.2015.08.016
- Cavallaro, A. Iannelli, L. Demasi, A. M. Razón “Phenomenology of Nonlinear Aeroelastic Responses of Highly Deformable Joined Wings”, Advances in Aircraft and Spacecraft Science, Vol. 2, No. 2, pp. 125-168, 2015, DOI: 10.12989/aas.2015.2.2.125
- Demasi, R. Cavallaro, F. Bertuccelli “Post-Critical Analysis of Joined Wings: the Concept of Snap-Divergence as a Characterization of the Instability”, Journal of Fluids and Structures, Vol. 54, pp. 701-718, 2015, DOI: 10.1016/j.jfluidstructs.2015.01.009
- Cavallaro, L. Demasi, A. Passariello “Nonlinear Analysis of PrandtlPlane Joined Wings: Effects of Anisotropy”, AIAA Journal, Vol. 52, No. 5, pp. 964-980, 2014, DOI: 10.2514/1.J052242
- Demasi, R. Cavallaro, and A. M. Razón, “Post-Critical Analysis of PrandtlPlane Joined-Wing Configurations”, AIAA Journal, DOI: 10.2514/1.J051700, Vol. 51, No. 1: pp 161-177, 2013.
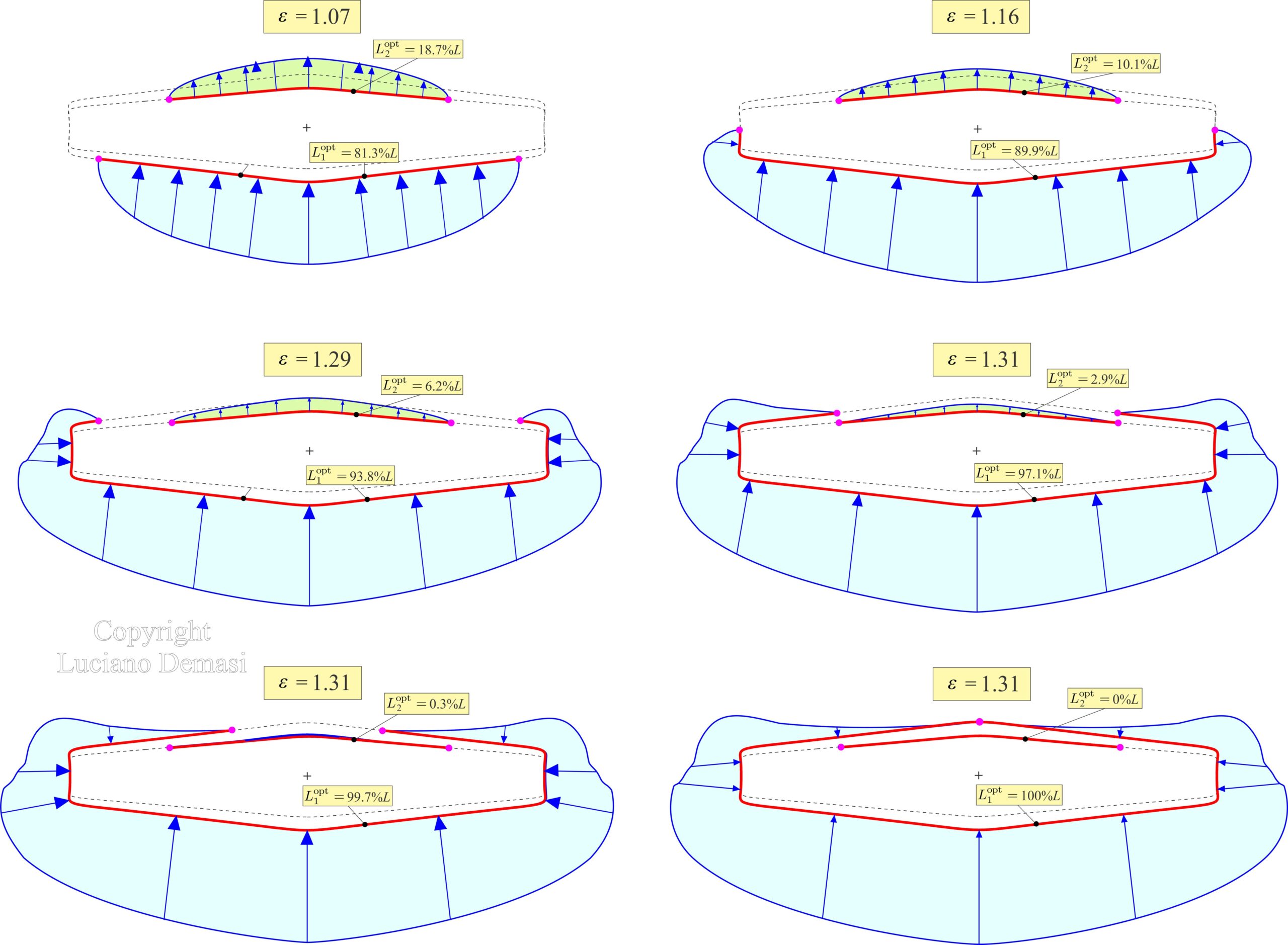
Minimization of Induced Drag of Airplanes
Dr. Demasi and co-authors introduced a configuration-invariant analytical formulation for the induced drag minimization of open and closed wing systems. An efficient computational method, ideal for the early conceptual phases of the design was introduced. The main results can be summarized as follows.
- When the lifting system has been translated into a single plane (Munk’s stagger theorem), the induced drag will be minimum when the component of the induced velocity normal to the lifting element at each point is proportional to the cosine of the angle of inclination of the lifting element at that point. The constant of proportionality is the ratio between the freestram velocity and the optimal aerodynamic efficiency (Augmented Munk’s Minimum Induced Drag Theorem). This theorem also olds for closed systems such as box wings and multi-wing systems.
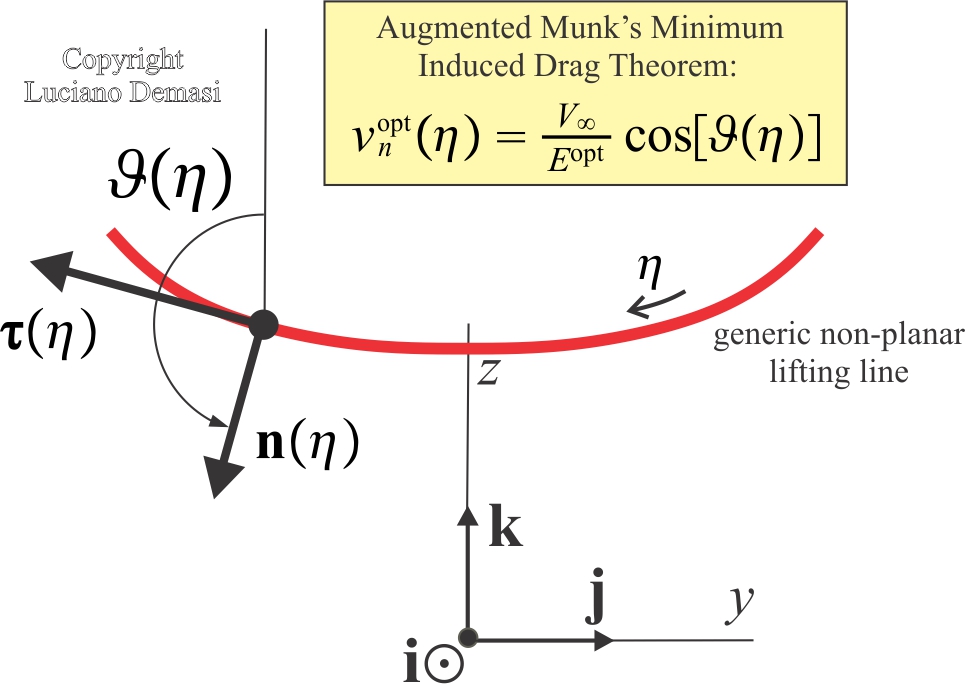
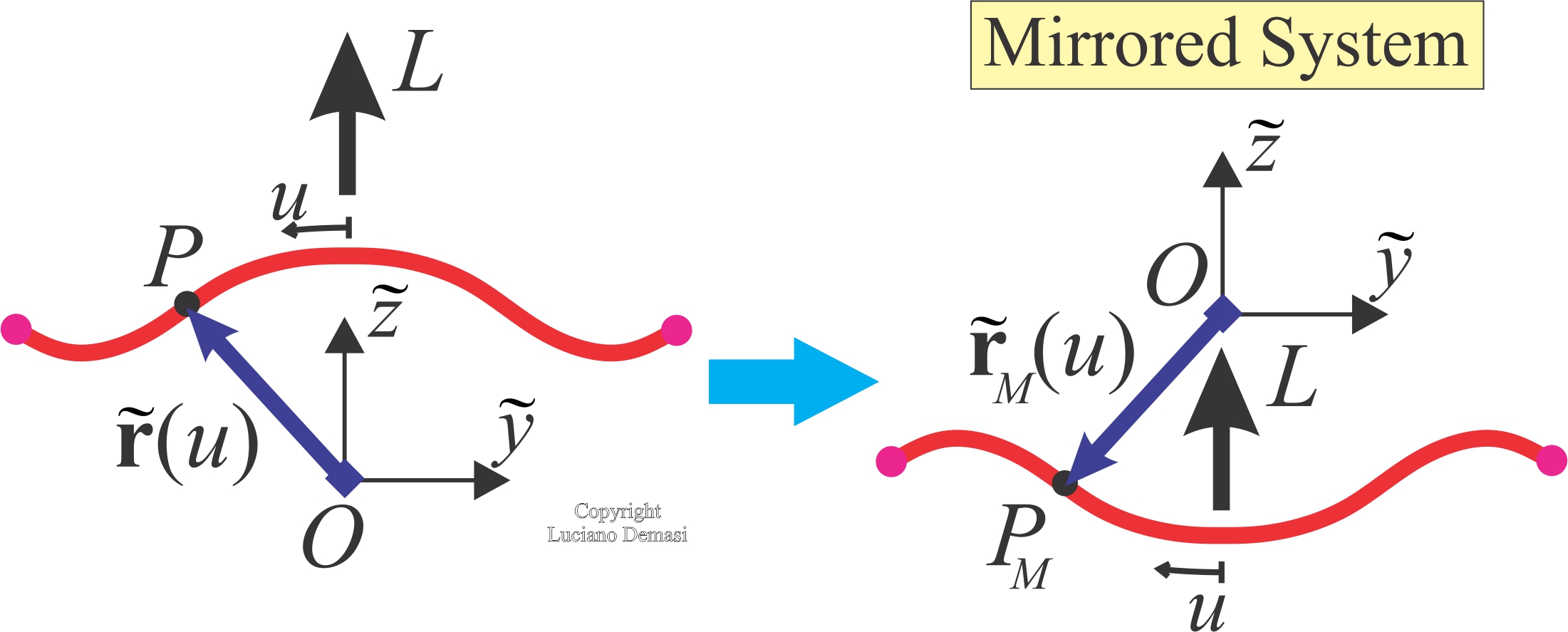
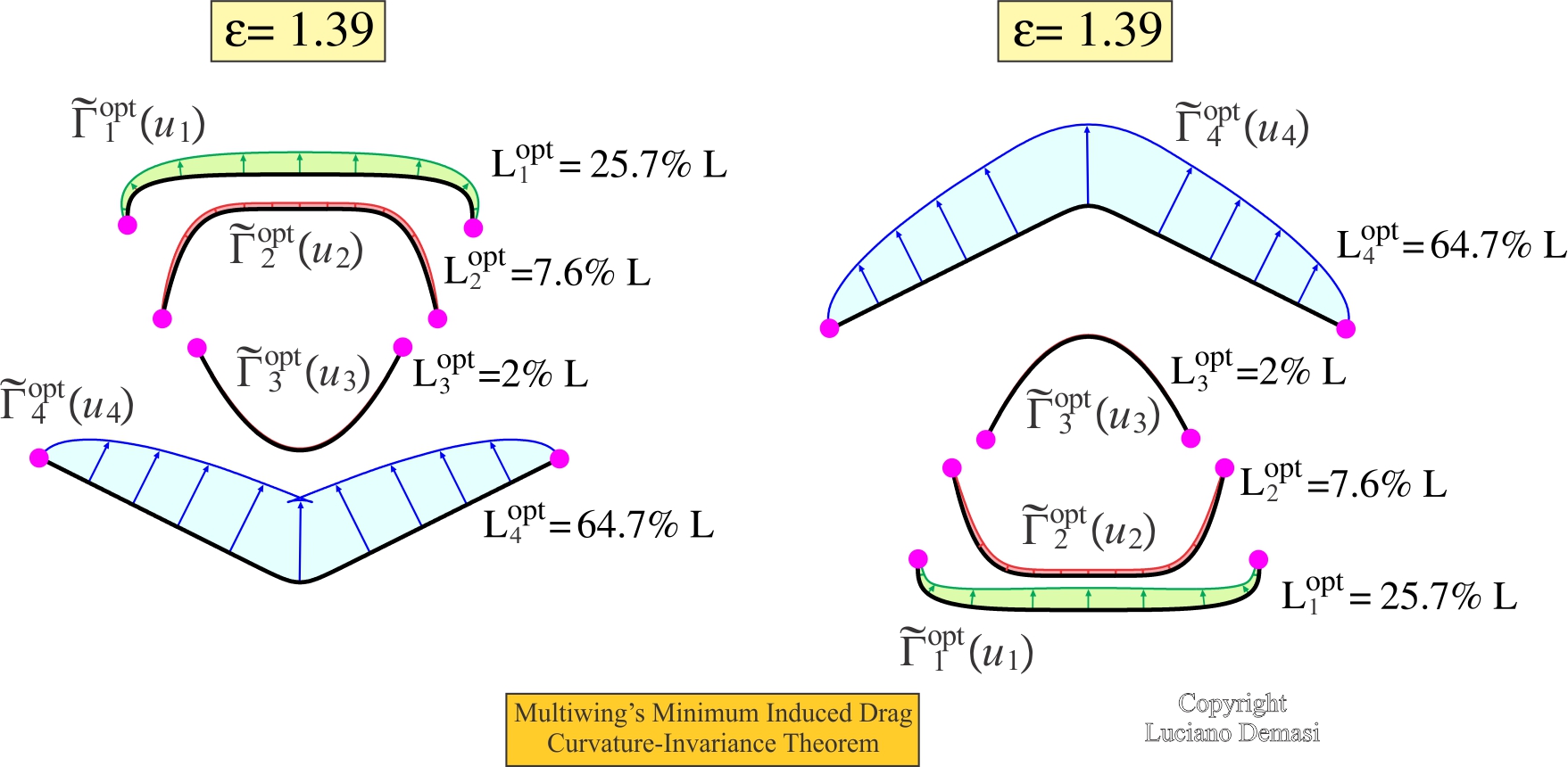
- Changing the sign of the curvature of the lifting line (i.e., the arc from convex is changed to concave or viceversa) does not modify the optimal induced drag and circulation distribution; the optimal solution is then invariant if the sign of the curvature is modified (Minimum Induced Drag Curvature-Invariance Theorem).
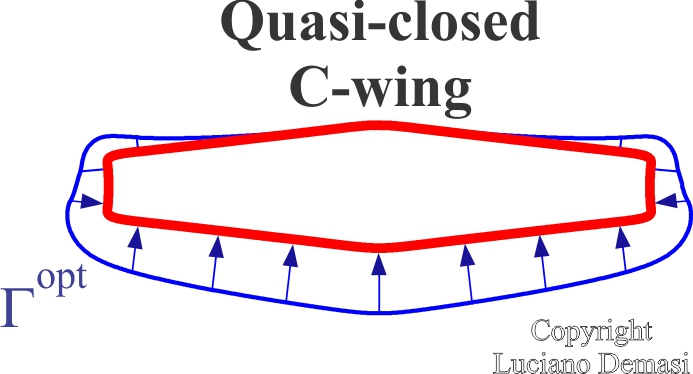
- If the two tips of a C wing are brought indefinitely close to each other, then both the optimal circulation and its first derivative tend to zero at those points (Quasi-closed C-Wing Zero-gradient Optimal Circulation Theorem)
- Given a closed wing system, the optimal circulation is indeterminate: there exists an infinite number of equivalent solutions obtained by adding an arbitrary constant to a reference optimal circulation. However, they all have the same optimal induced drag and the same optimal circulation lift (Closed System’s Indeterminate Optimal Circulation Theorem)
- The optimal induced drag of a C-wing is equal to the one relative to the corresponding closed wing system, when the tips of the C-wing are smoothly brought indefinitely close to each other. The resulting optimal circulation is the findamental optimal circulation for the closed wing system for the case (Closed System’s C-Wing Limit Theorem)
- In a general multiwing under optimal conditions, the aerodynamic efficiency of each wing is equal to the aerodynamic efficiency of the entire system. This theorem holds even if the wings are not the same and present different shapes and wingspans (Multiwing Minimum Induced Drag Theorem). Corollary of this theorem: in a general multiwing under optimal conditions and subjected to a positive lifting force (constraint), the aerodynamic lift on each wing cannot be negative.
- A wing system defined by a closed and smooth curve can always be considered as a biwing formed by two disjoint wings, whose tips are smoothly brought indefinitely close to each other, so that the limit biwing coincides with the original smooth curve. This biwing provides the same optimal induced drag of the corresponding closed wing system. In particular, the biwing provides the closed wing’s fundamental circulation distribution. The origin of the closed curve is on any of the biwing system’s tips (Closed Systems’s Biwing Limit Theorem).
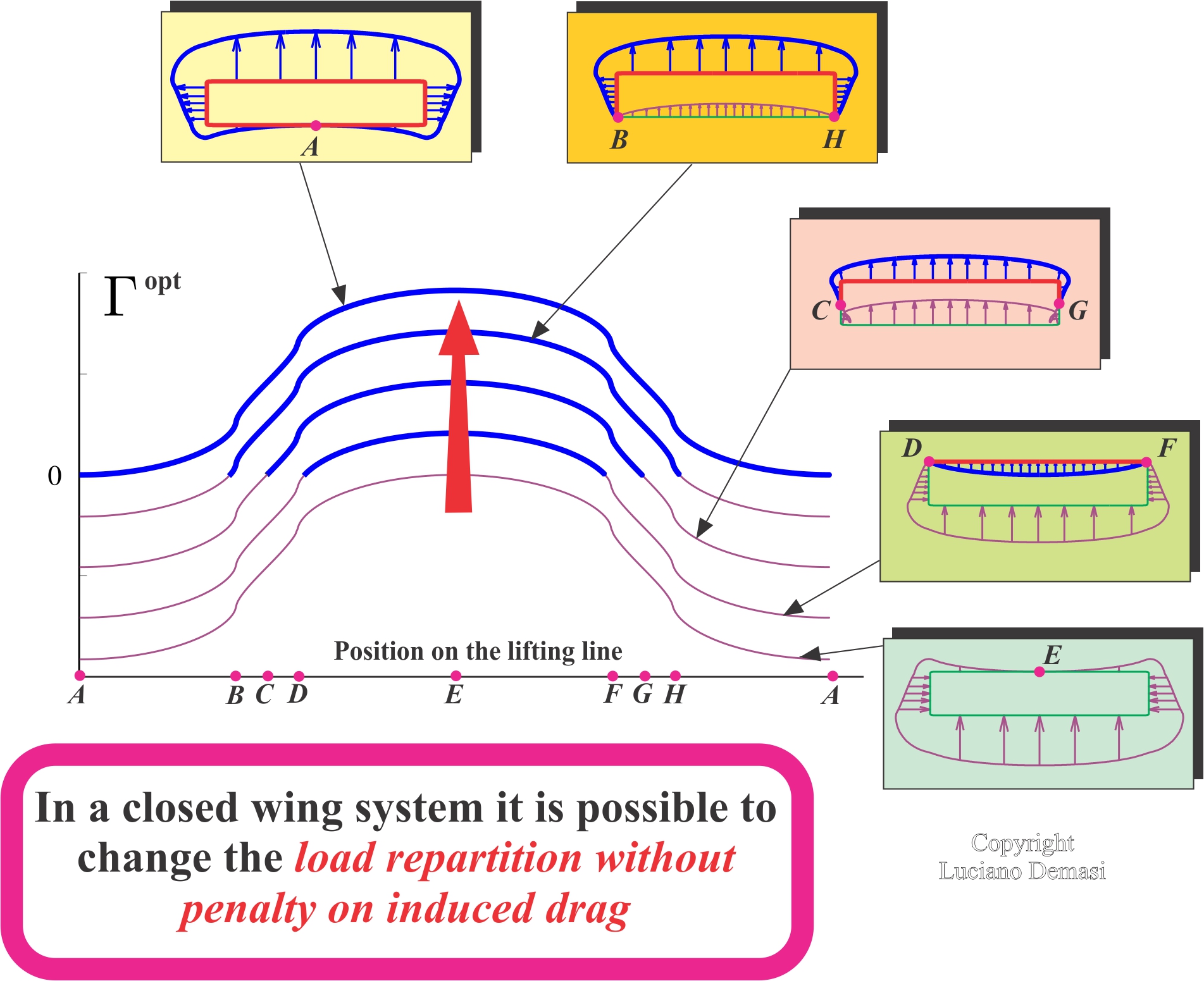
- Given a multiwing with an arbitrary number of generic nonplanar wings, the optimal circulations, load repartitions, and induced drag do not change if all lifting lines are replaced with symmetric (with respect to y) counterparts (Multiwing’s Minimum Induced Drag Curvature-Invariance Theorem).
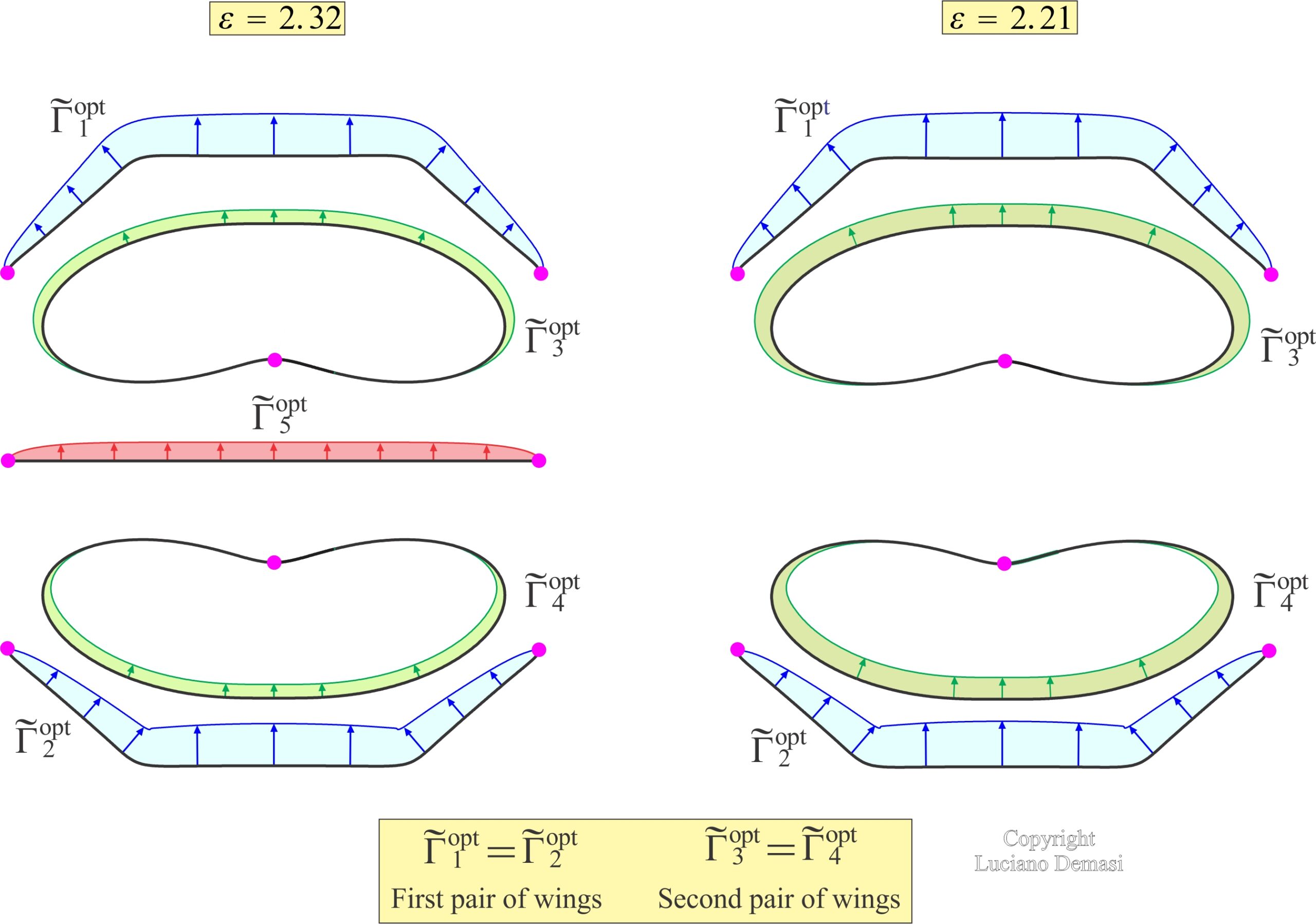
- In a symmetric multiwing, the circulations of two wings (pair) symmetrically located with respect to the y axis are the same under optimal conditions (Symmetric Multiwing Optimal Circulation Theorem).
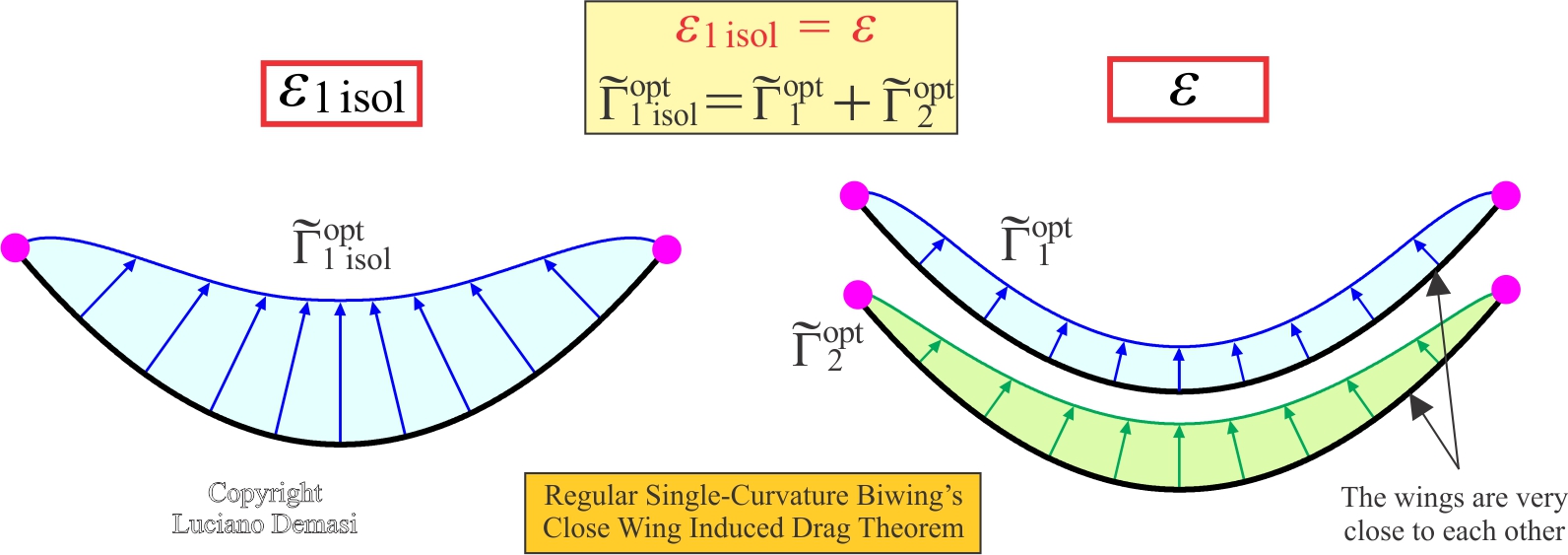
- When the two wings of a regular single-curvature biwing are brought very far from each other, the optimal circulations over the two wings are no longer different: they are the same. Moreover, the optimal induced drag of the system is exactly half of the optimal induced drag of that one would obtain if either wing was considered as an isolated indeendent system subjected to the same lift (Regular Single-Curvature Biwing Far Wing Induced Drag Theorem).
- When the two wings of a regular single-curvature biwing are borught very close to each other (but still at a finite distance), the optimal circulations over the two wings are different, but their summation asymptotically equals the optimal circulation of the corresponding single-wing system. Moreover, the optimal induced drag of the biwing is aymptotically equal to the optimal induced drag that one would obtain if either wing was considered as an isolated independent system subjected to the same lift (Regular Single-Curvature Biwing Close Wing Induced Drag Theorem).
- If the two wings of an asymmetric biwing are brought very far from each other, then the optimal conditions of each wing are equal to the corresponding optimal conditions of the wings considered as isolated systems (Asymmetric Biwing’s Far Wing Induced Drag Theorem).
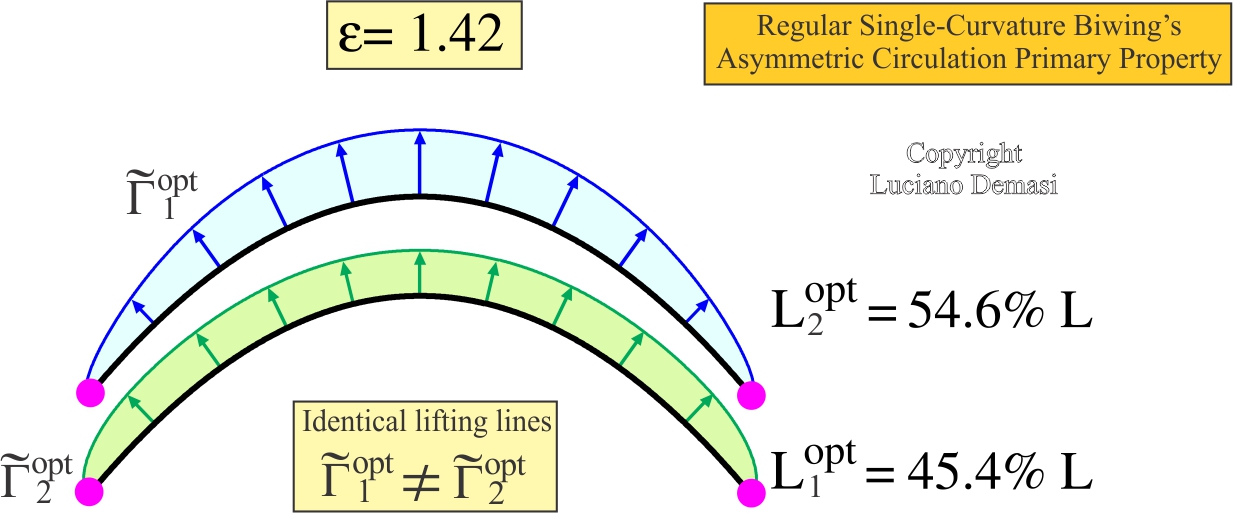
- If the lifting lines of a biwing are obtained from a rigid translation of the same nonplanar curve (fundamental curve) in the direction of the lift, then the optimal circulation distributions over the two sings are always different when there is a finite distance between the wings (Regular Single-Curvature Biwing Asymmetric Circulation Primary Property).
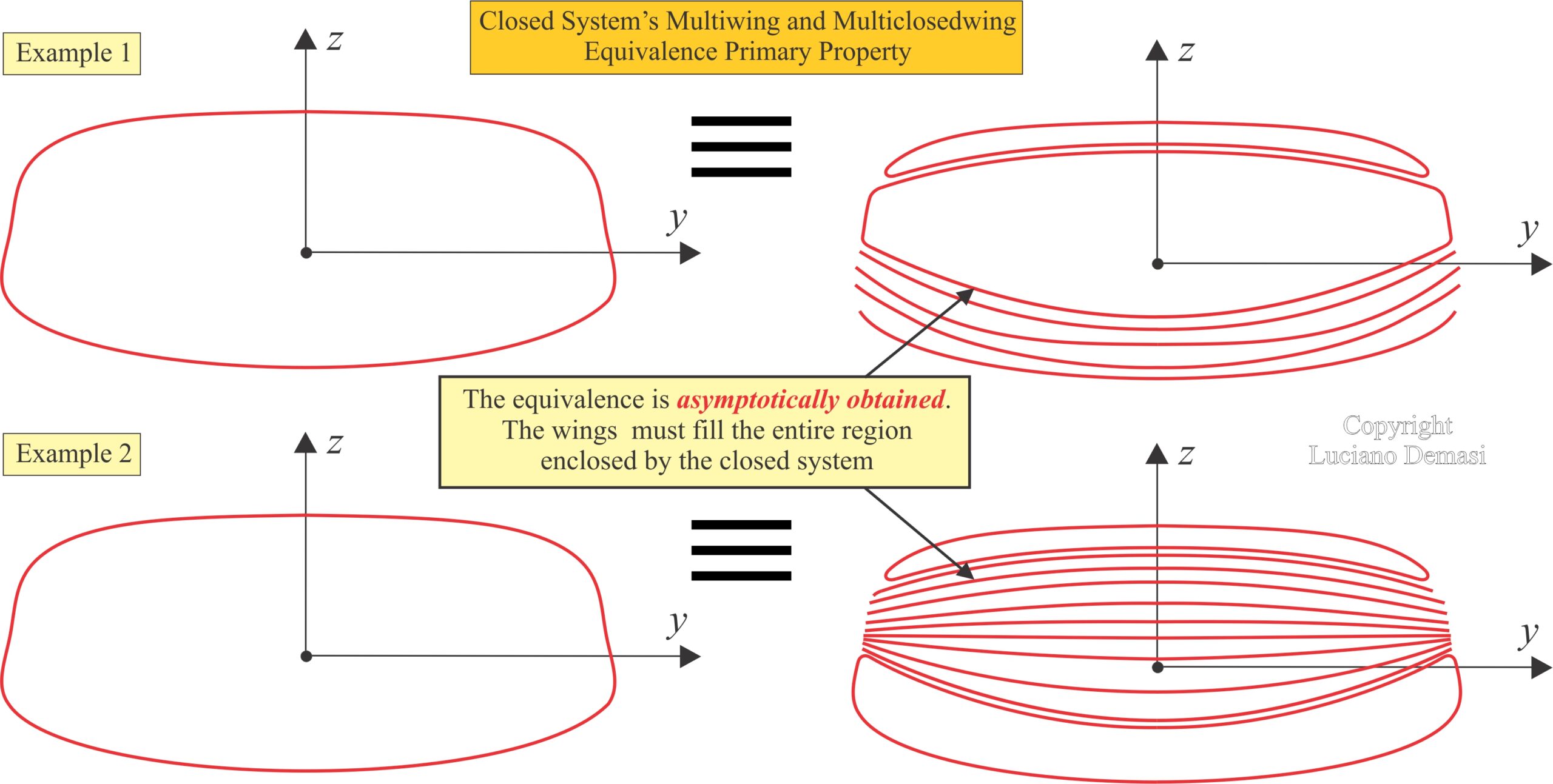
- A closed system presents the same optimal induced drag of the combination of a multiwing with an infinite number of wings and a inite number of closed wings. The closed wings must be tangent to the curve of the corresponding closed system. All the wing tips of the multiwing must be on the curve l of the corresponding closed system (Closed-System’s Multiwing and Multiclosedwing Equivalence Primary Property).
- Assume that the dimensionless fundamental optimal circulation of a closed system (with a given parametrization for the lifting line l) is known. Consider now another wing system made of two wings. The first wing is the closed-wing lifting line l. The second wing is represented any wing with any shape (closed or open) included in the region eclosed by l. Then, the optimal conditions for this second system consist of a zero circulation over the internal wing and the same circulation for the external closed wing. The two systems present the same optimal induced drag (Closed System’s Internal WingZero Circulation Primary Property).

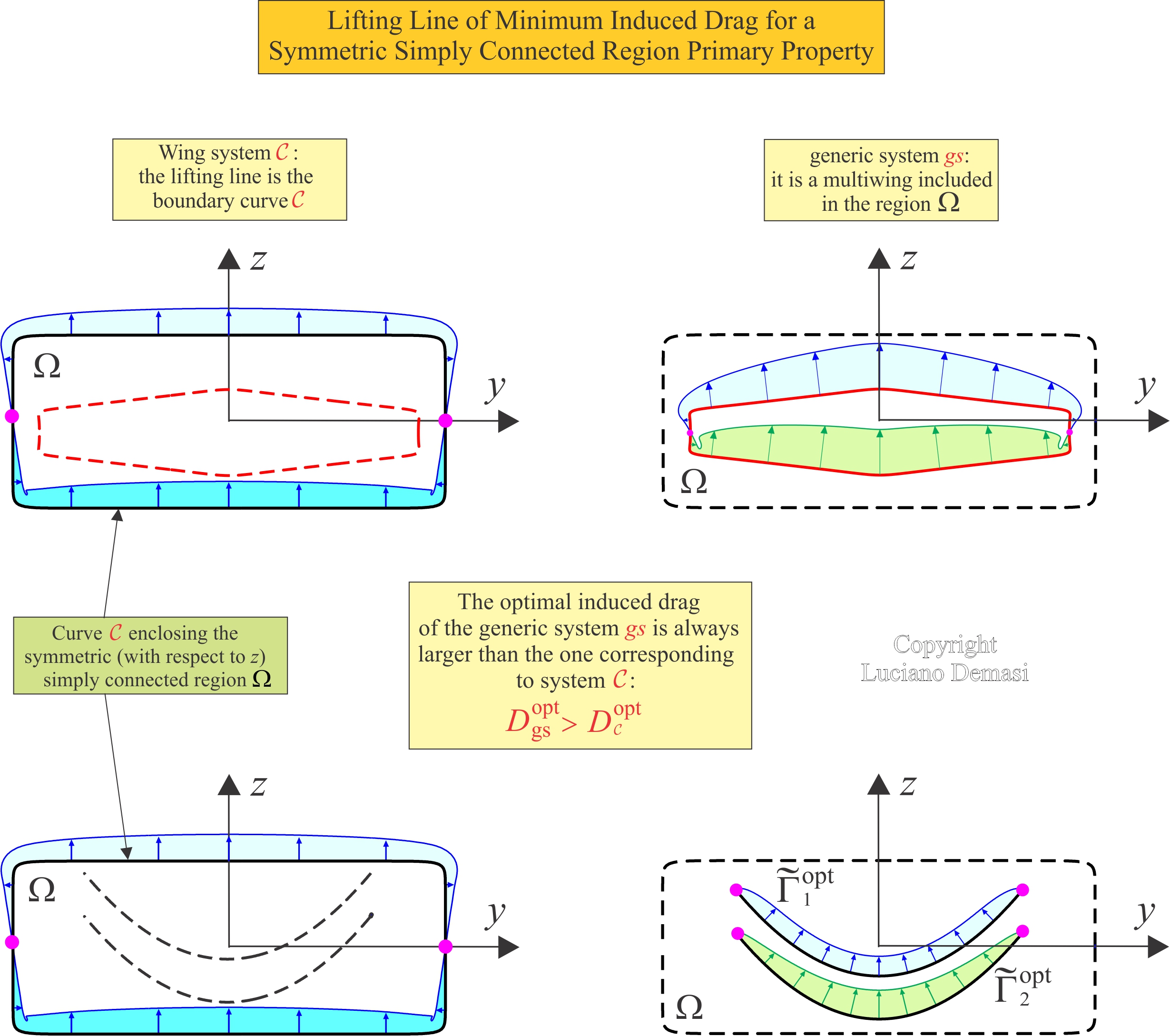
- For a given lift L, any multiwing entirely included in a symmetric (with respect to z) simply connected region W will have a larger induced drag than the one corresponding to the closed system whose lifting line is C, boundary of W (Lifting Line of Minimum Induced Drag for a Symmetric Simply Connected Region Primary Property).
- Given a truss-braced wing with m juries (because of the symmetry with respect to the x-z plane, the number of juries is determined by considering only half of the wing), the optimal circulation is indeterminate; there exist equivalent solutions obtained by adding, to a reference circulation distribution, arbitrary constant circulations in all the m + 1 symmetric, with respect to the x-z plane, simply connected lifting-line paths which can be identified within the wing system (Truss-Braced Wing Indeterminate Optimal Circulation Primary Property).
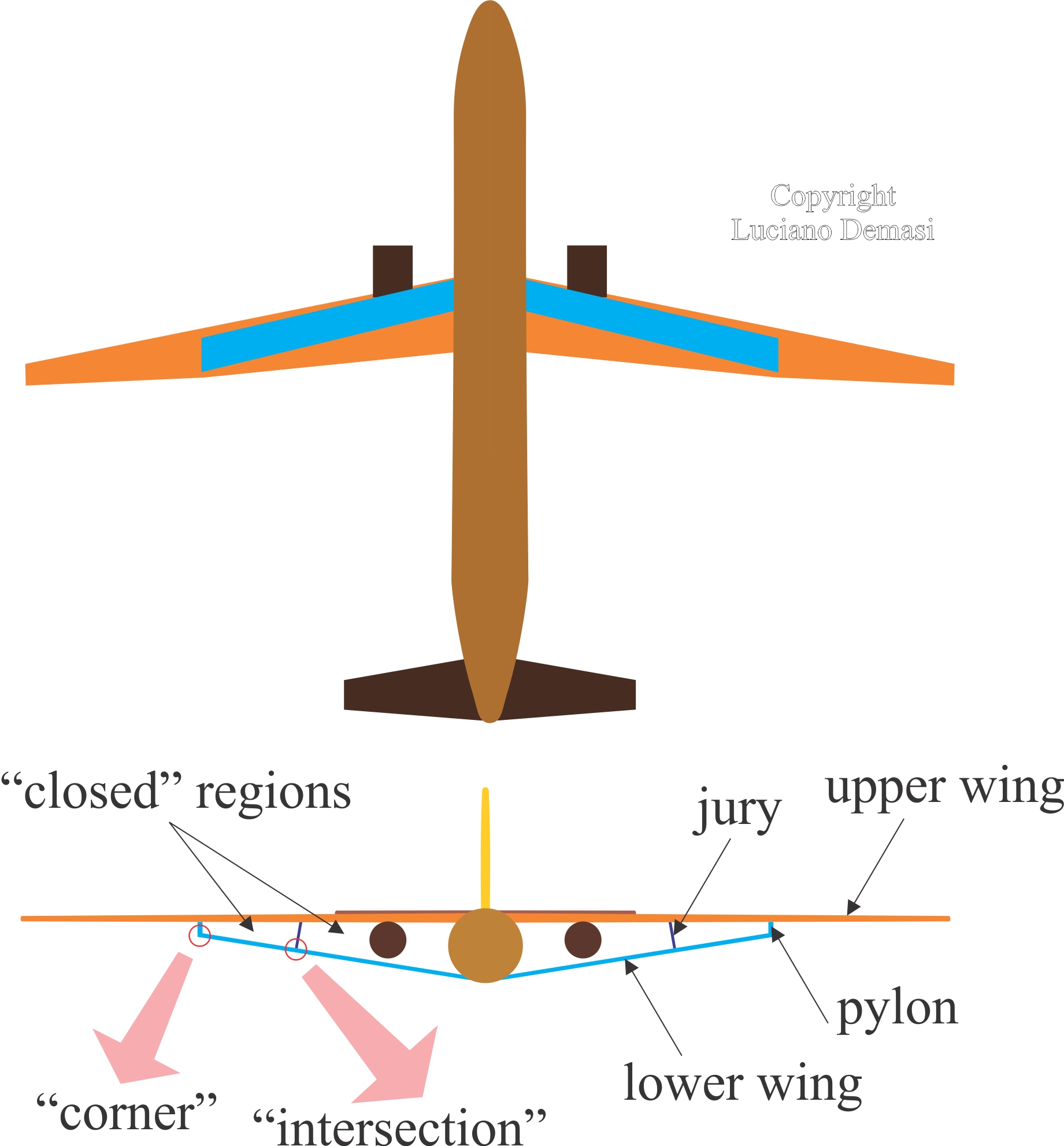
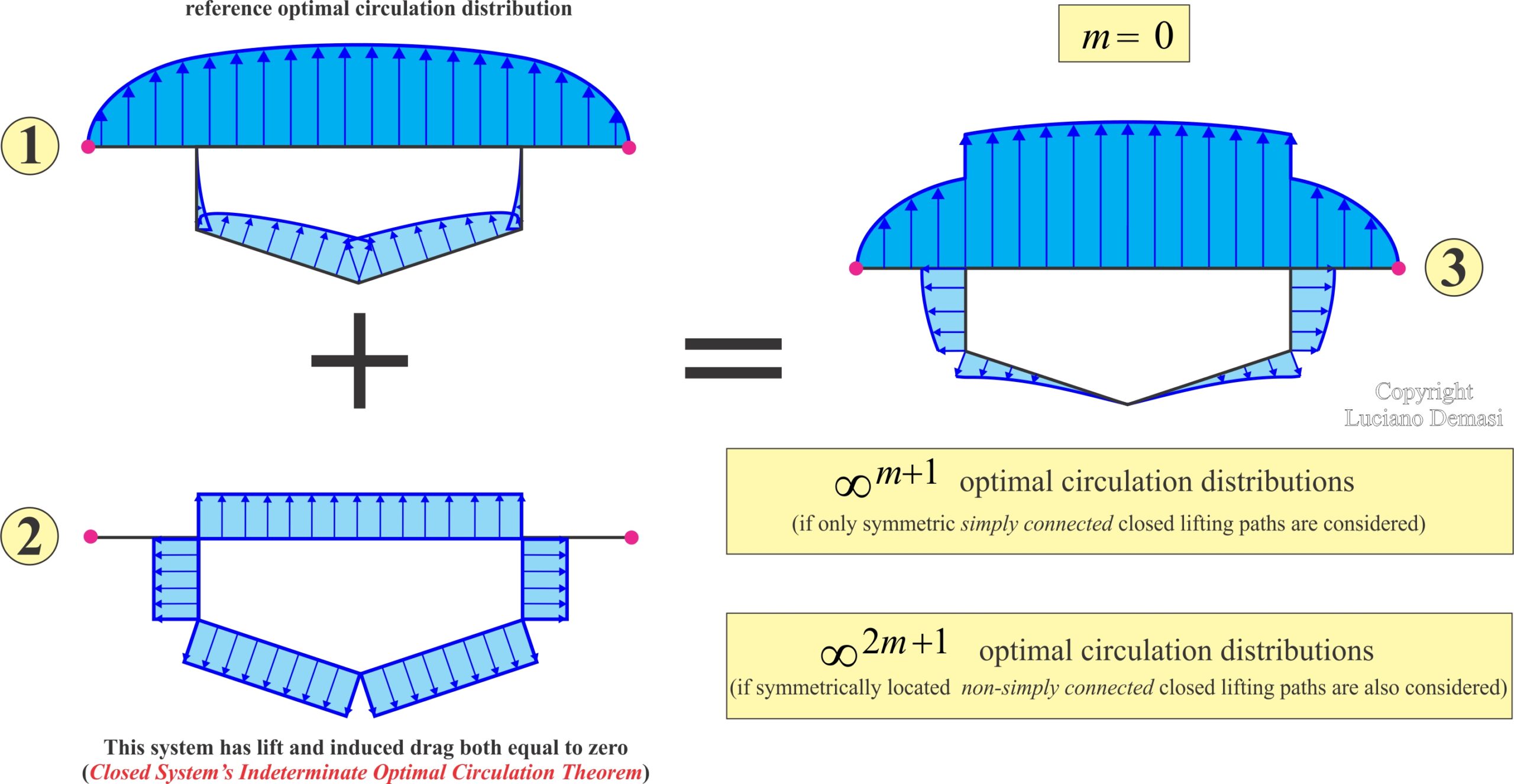
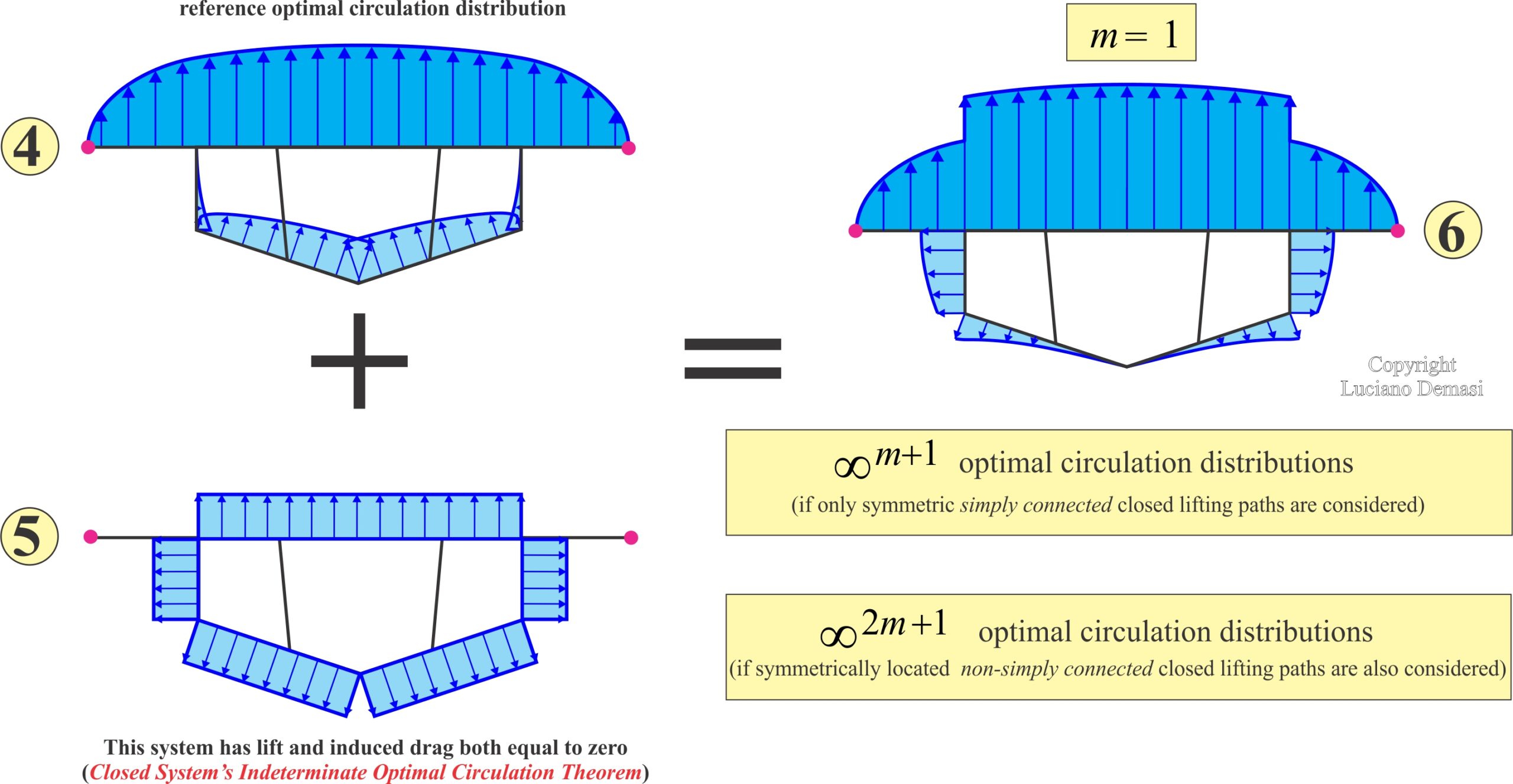
- Given a truss-braced wing with m>0 juries, the optiaml circulation on each jury is either zero or at most constant (Truss-Braced Wing Jury Constant Load Primary Property).
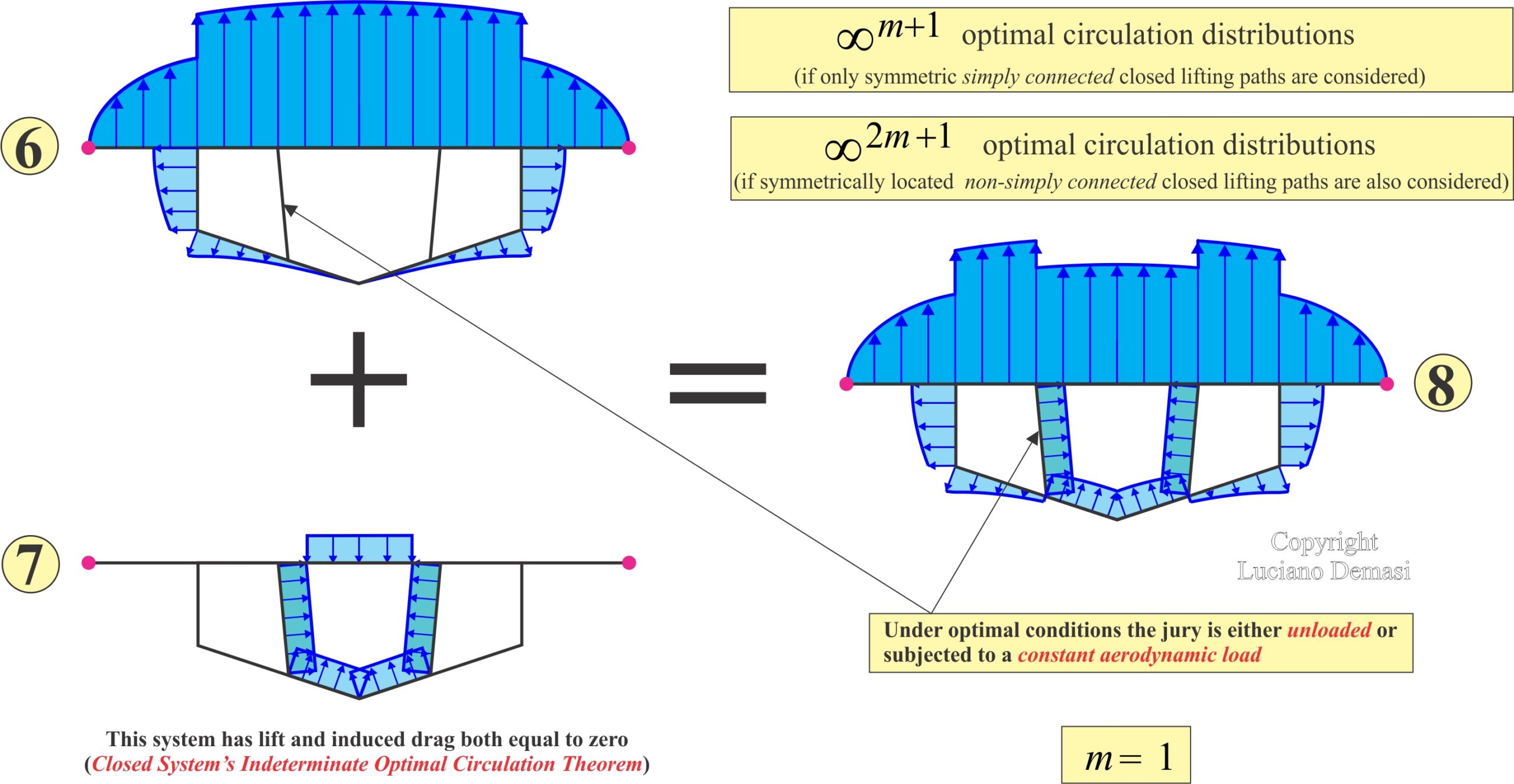
- Given a truss-braced with juries, the optimal induced drag value coincides with the value obtained with the corresponding strut-braced wing (Truss- and Strut-Braced wing Induced Drag Equivalence Primary Property)
- The induced drag of Box Wings immersed in viscous and compressible flows is equal to the one predicted by inviscid and incompressible theories, even in presence of shock waves (this property has been verified for Box Wings with vertical aspect ratios of 0.2 and 0,4).
- The induced drag minimization problem, for a generic nonplanar open wing system, presents a global optimum. Moreover, this property holds also for the less common asymmetric wings.
Selected Publications
- Demasi, A. Dipace, G. Monegato, and R. Cavallaro, “Invariant Formulation for the Minimum Induced Drag Conditions of Non-planar Wing systems”, AIAA Journal, Vol. 52, No. 10, pp. 2223-2240, 2014, DOI: 10.2514/1.J052837
- Junghanns, G. Monegato, L. Demasi “Properties and Numerical Solution of an Integral Equation System to Minimize Airplane Drag for a Multiwing System”, 2020, Mathematical Methods in the Applied Sciences, 1-24, DOI: 10.1002/mma.6786
- Russo, R. Tognaccini, L. Demasi, “Box Wing and Induced Drag: Compressibility Effects in Subsonic and Transonic Regimes”, AIAA Journal, Vol. 58, No. 6, 2020, DOI: 10.2514/1.J059080
- Demasi, G. Monegato, R. Cavallaro, R. Rybarczyk “Minimum Induced Drag Conditions for Truss-Braced Wings”, AIAA Journal, Vol. 56, No. 12, pp. 4669-4684, 2018, DOI: 10.2514/1.J057225
- Demasi, G. Monegato, R. Cavallaro “Minimum Induced Drag Theorems for Multi-Wing Systems”, AIAA Journal, Vol. 55, No. 10, pp. 3266-3287, 2017, DOI: 10.2514/1.J055652
- Demasi, G. Monegato, A. Dipace, R. Cavallaro “Minimum Induced Drag Theorems for Joined Wings, Closed Systems, and Generic Biwings: Theory”, Journal of Optimization Theory and Applications, Vol. 169, 1, pp-200-235, 2016,DOI: 10.1007/s10957-015-0849-y
- Demasi, G. Monegato, E. Rizzo, R. Cavallaro A. Dipace, “Minimum Induced Drag Theorems for Joined Wings, Closed Systems, and Generic Biwings: Applications”, Journal of Optimization Theory and Applications, Vol. 169, 1, pp-236-261, 2016, DOI: 10.1007/s10957-015-0850-5
- Russo, E. Saetta, R. Tognaccini, G. Dacome, L. Demasi “Aerodynamic Analysis of a Box Winglet: Viscous and Compressible Flow Predictions”, Aerotecnica Missili & Spazio, Vol 101 (4), 321-334, 2022, DOI: 10.1007/s42496-022-00125-6
- Demasi, G. Monegato, R. Cavallaro, R. Rybarczyk “Optimum Induced Drag of Wingtip Devices: the Concept of Best Winglet Design”, Aerotecnica Missili & Spazio, Vol 101 (1), 61-93, 2022, DOI: 10.1007/s42496-022-00110-z
Honors and Awards
- Outstanding Contribution to Aerospace Research (2023)
American Institute of Aeronautics and Astronautics (AIAA)
Ranked in top 2% of authors worldwide
The study, which is conducted annually at Stanford University, creates a publicly available comprehensive database of 100,000 top scientists in 22 scientific fields and 176 subfields. Based on career-long impact Luciano Demasi is ranked No. 166 over a total of 55.422 authors worldwide in the subfield of Aerospace & Aeronautics [https://elsevier.digitalcommonsdata.com/datasets/btchxktzyw/6].
- Associate Fellow-Class of 2019 in the American Institute of Aeronautics and Astronautics (AIAA)
ASSOCIATE FELLOWS shall be persons who have accomplished or been in charge of important engineering or scientific work, or who have done original work of outstanding merit, or who have otherwise made outstanding contributions to the arts, sciences, or technology of aeronautics or astronautics. Each year, only one for every 150 voting members are selected and approved.
[https://www.aiaa.org/].
- Thomson Highly Cited Researcher, section ”Materials Science”
This Highly Cited Research resource captured the people behind the most influential publications in 21 broad subject categories in life sciences, medicine, physical sciences, engineering and social sciences based on citation metrics. Within their category, these individuals represent less than one-half of one percent of all publishing researchers—truly an extraordinary accomplishment [http://highlycited.com].
- Collier Research HyperSizer/AIAA Structures best paper award (2013)
- Composite Structures award for the best paper of the year (2010)
- M.S in Aerospace Engineering with final grade of 110/110 Magna cum Laude
(Award for Excellence)
- First author, in 25 years of history of the journal, to have a series of five papers published at once and without any required change in the peer-reviewed journal Composite Structures. The comments that were received from the reviewers were the following:
“A major and timely treatise on composite plate theories which will be widely welcomed by the composites community. An easy to understand comparison of composite plate analytical methodologies which succinctly explains the subtleties in more complex problems”.
“An exceptional contribution to knowledge in laminated plate theory which deserves a wide audience.
The most outstanding contribution to composite structures this reviewer has had the pleasure of assessing for some time”.
“May I add that I greatly enjoyed reading your papers and am sure that they will be widely appreciated. They break new ground in being the first series of five papers since the Journal began 25 years ago. Also although occasionally papers are accepted for publication without changes being required, this is unusual. It is very unusual for a series of two papers to be accepted in this way, which makes a series of five “exponentially unlikely!”
- Italian Habilitation (Full Professorship in Aerospace Engineering) (Feb 2014)
- Most Influential Faculty (Undergraduate teaching award, May 2012)
- Most Influential Faculty (Undergraduate teaching award, May 2013)
- Most Outstanding Aerospace Eng. Faculty (Undergraduate teaching award, May 2014)
- Most Influential Faculty (Undergraduate teaching award, May 2015)
The complete Luciano Demasi’s resume can be downloaded here.